[Algorithm][Binary Search] 이진 탐색(BS) 개념 및 구현

순서

I. 이진 탐색(Binary Search) 이란? (이하 BS)

II. BS의 기본 원리

III. BS 구현 코드

---

I. 이진 탐색(Binary Search) 이란?

기본적으로 이름에서 나타나듯 탐색이다.

[2,4,6,8,10] 이라는 배열이 있을 때 특정 숫자가 존재하는지 아닌지 판단하는 것이다.

그렇다면 왜? 이진 탐색을 할까? for문 돌리면 되지 않나...?

정답은, 시간 복잡도 때문이다.

현재는 5개의 데이터만 있지만 1e8개, 1e20개가 있다면 O(N)의 시간복잡도로는 턱없이 부족하다.

따라서 O(Log2(N))의 이진 탐색을 사용하는 것이다.

 방법은 간단히 말해,
크기 순서대로 정렬한 뒤 크기를 비교해가며 절반씩 탐색 범위를 좁힌다. -> Log2

 

이진탐색은 단순히 탐색 뿐 아니라, 상한가 하한가를 찾는 문제로 응용되기도 한다.

 

---

II. BS의 기본 원리

우리는 앞서 절반씩 탐색 범위를 좁힌다는 것을 알게되었다.

그렇다면 그 순서는 어떻게 될까?

우선 똑같은 탐색을 끝까지 반복하기 때문에 "재귀함수" 혹은 "While문"을 사용한다.

또한, 탐색 범위가 절반씩 줄어들기 때문에
배열의 인덱스를 나타내는 인자가 3개 필요하다.
start, mid, end이고 mid = int ( (start+end)/2 ) 이다.

또한 탐색의 기준은 mid인덱스가 된다.

---

1. 탐색에 성공 했을 때

s=0, e=5, m=2로 시작

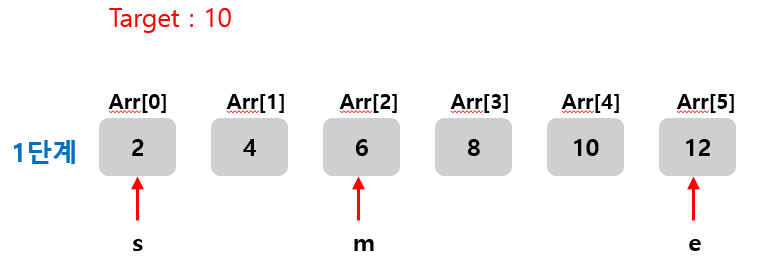
Arr[m] = 6으로 타겟인 10보다 작다.

따라서 m의 오른쪽으로 탐색 범위를 절반 좁혀주게 되는 과정을 거친다.

s = m+1, e = e, m = (s+e)/2
s = 3, e = 5, m = 4

s=3, e=5, m=4로 업데이트

Arr[m] = 10으로 10을 찾았다.

반환.

 

---

2. 탐색에 실패 했을 때

s=0, e=6, m=3으로 시작

Arr[m] = 8로 타겟인 5보다 크다.

따라서 m의 왼쪽으로 탐색 범위를 절반 좁혀주는 과정을 거친다.

s=s, e=m-1, m=(s+e)/2
s=0, e=2, m=1

 

s=0, e=2, m=1로 업데이트

Arr[m] = 4로 타겟인 5보다 작다.

따라서 m의 오른쪽으로 탐색 범위를 절반 좁혀주는 과정을 거친다.

s=m+1, e=e, m=(s+e)/2
s=2, e=2, m=2

 

s=e=m = 2로 업데이트

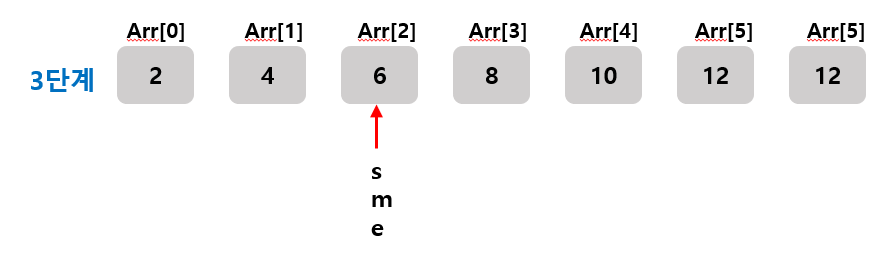
Arr[m] = 6으로 타겟인 5보다 크다.

모든 탐색의 마지막은 양 끝인 s,e를 탐색할 때 이므로
(m = s 혹은 m=e 일 때)

여기서 위와 같이 마지막 탐색 후 성공하지 못한 경우
s==e 조건으로 실패로 반환해도 된다. (재귀함수 경우)

한 단계 더 들어가서
e<s 가 되는 경우로 반환 할 수도 있다. (While문 경우)

이전 단계처럼 m의 왼쪽으로 탐색 범위를 좁혀주는 과정을 진행하면,

s=2, e=1이 된다.

 

e < s로 위치 역전 되었으므로 탐색 실패

다음 단계로 들어왔을 때 상태가 e<s 이다. 따라서 탐색 실패 반환.

 

---

III. BS 구현 코드

1. While문으로 구현

<hide/>
#include <algorithm>
#include <iostream>
using namespace std;

int Arr[7] = {2,4,6,8,10,12,14};
int target = 5;

int main(){
	int s,m,e;
    int findTgt =0;
    
    sort(&Arr[0], &Arr[0+7]);
    
    s = 0;
    e = 6;
    m = (s+e)/2;
    
    while(s<=e){
    	if(Arr[m] == target){
            findTgt = 1;
            break;
        }
        // 타겟이 오른쪽에 있을 때
        if(Arr[m] < target){
        	s = m+1;
            m = (s+e)/2;
        }
        // 타겟이 왼쪽에 있을 때
        else if(Arr[m] > target){
            e = m-1;
            m = (s+e)/2;
        }
    }
    
    if(findTgt) cout<<target<<" is in Arr[]"<<endl;
    else cout<<target<<" is not in Arr[]"<<endl;
    
    return 0;
}

 

2. 재귀함수로 구현

<hide/>
#include <algorithm>
#include <iostream>
using namespace std;

int Arr[7] = {2,4,6,8,10,12,14};
int target = 5;

int BinarySearch(int s, int e){

    // if (e<s) return 0; s==e조건 빼고 이렇게 놔도 된다.
    // 그러나 1단계 더 들어오게 된다.
    
    int m = (s+e)/2;
    
    if( Arr[m] == target ) return 1;
    
    if( s==e ) return 0;
    
    // 타겟이 오른쪽에 있을 때
    if(Arr[m] < target)    return BinarySearch(m+1,e);
        
    // 타겟이 왼쪽에 있을 때
    else if(Arr[m] > target) return BinarySearch(s,m-1);

}

int main(){
	int s,e;
    int findTgt =0;
    
    sort(&Arr[0], &Arr[0+7]);
    
    s = 0;
    e = 6;
    
    findTgt = BinarySearch(s,e);
    
    if(findTgt) cout<<target<<" is in Arr[]"<<endl;
    else cout<<target<<" is not in Arr[]"<<endl;
    
    return 0;
}